19 marzo, 20075 diciembre, 2014 by doblevia

Curvas Circulares Simples

Las curvas circulares simples se definen como arcos de circunferencia de un solo radio que son utilizados para unir dos alineamientos rectos de una vía.

Una curva circular simple (CCS) está compuesta de los siguientes elementos:

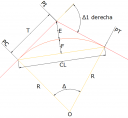
Ángulo de deflexión [Δ]: El que se forma con la prolongación de uno de los alineamientos rectos y el siguiente. Puede ser a la izquierda o a la derecha según si está medido en sentido anti-horario o a favor de las manecillas del reloj, respectivamente. Es igual al ángulo central subtendido por el arco (Δ).
Tangente [T]: Distancia desde el punto de intersección de las tangentes (PI) -los alineamientos rectos también se conocen con el nombre de tangentes, si se trata del tramo recto que queda entre dos curvas se le llama entretangencia– hasta cualquiera de los puntos de tangencia de la curva (PC o PT).
$T=R\cdot\tan(\frac{\Delta}{2})$

Radio [R]: El de la circunferencia que describe el arco de la curva.
$R=\frac{T}{\tan\frac{\Delta}{2}}$
Cuerda larga [CL]: Línea recta que une al punto de tangencia donde comienza la curva (PC) y al punto de tangencia donde termina (PT).
$CL=2\cdot{R}\sin\frac{\Delta}{2}$
Externa [E]: Distancia desde el PI al punto medio de la curva sobre el arco.
$E=T\tan\frac{\Delta}{4}$

$E=R(\frac{1}{\cos(\frac{\Delta}{2})}-1)$
Ordenada Media [M] (o flecha [F]): Distancia desde el punto medio de la curva hasta el punto medio de la cuerda larga.
$M=R(1-\cos\frac{\Delta}{2})$
Grado de curvatura [G]: Corresponde al ángulo central subtendido por un arco o una cuerda unidad de determinada longitud, establecida como cuerda unidad (c) o arco unidad (s). Ver más adelante para mayor información.
$G_c = 2\arcsin\frac{c}{2R}$
Longitud de la curva [L]: Distancia desde el PC hasta el PT recorriendo el arco de la curva, o bien, una poligonal abierta formada por una sucesión de cuerdas rectas de una longitud relativamente corta. Ver más adelante para mayor información.
$L_c=\frac{c\cdot\Delta}{G_c}$

Ahora vamos a detenernos en dos aspectos con un poco más de detalle:

Grado de curvatura

Usando arcos unidad:

En este caso la curva se asimila como una sucesión de arcos pequeños (de longitud predeterminada), llamados arcos unidad (s). Comparando el arco de una circunferencia completa (2πR), que subtiende un ángulo de 360º, con un arco unidad (s), que subtiende un ángulo G_s (Grado de curvatura) se tiene:

$\frac{2\pi R}{360^\circ}=\frac{s}{G_s}$

$entonces: G_s=\frac{180\cdot s}{\pi R}$

Usando cuerdas unidad:

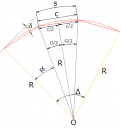
Este caso es el más común para calcular y materializar (plasmar en el terreno) una curva circular, pues se asume que la curva es una sucesión de tramos rectos de corta longitud (también predeterminada antes de empezar el diseño), llamados cuerda unidad (c). La continuidad de esos tramos rectos se asemeja a la forma del arco de la curva (sin producir un error considerable). Este sistema es mucho más usado porque es más fácil medir en el terreno distancias rectas que distancias curvas (pregunta: ¿Se pueden medir distancias curvas en el terreno utilizando técnicas de topografía?¿cómo?).

Tomando una cuerda unidad (c), inscrita dentro del arco de la curva se forman dos triángulos rectángulos como se muestra en la figura, de donde:

$\sin\frac{G_c}{2}=\frac{c/2}{R}$

$\rightarrow G_c = 2\arcsin\frac{c}{2R}$

Longitud de la curva

A partir de la información anterior podemos relacionar longitudes con ángulos centrales, de manera que se tiene:

Usando arcos unidad:

$\frac{2\pi R}{360^\circ}=\frac{L_s}{\Delta}$

$\rightarrow L_s=\frac{\Delta\pi R}{180}$

Usando cuerdas unidad:

$\frac{L_c}{\Delta}=\frac{c}{G_c}$

$\rightarrow L_c=\frac{c\Delta}{G_c}$

La longitud de una cuerda unidad, o de un arco unidad, se toma comúnmente como 5 m , 10 m , ó 20 m .

Localización de una curva circular

Para calcular y localizar (materializar) una curva circular a menudo se utilizan ángulos de deflexión.

Un ángulo de deflexión (δ) es el que se forma entre cualquier línea tangente a la curva y la cuerda que va desde el punto de tangencia y cualquier otro punto sobre la curva.

Como se observa en la figura, el ángulo de deflexión (δ) es igual a la mitad del ángulo central subtendido por la cuerda en cuestión (Φ).

Entonces se tiene una deflexión para cada cuerda unidad, dada por:

${\delta}_c=\frac{G_c}{2}$

Es decir, se puede construir una curva con deflexiones sucesivas desde el PC, midiendo cuerdas unidad desde allí. Sin embargo, rara vez las abscisas del PC o del PT son cerradas (múltiplos exactos de la cuerda unidad), por lo que resulta más sencillo calcular una subcuerda desde el PC hasta la siguiente abscisa cerrada y, de igual manera, desde la última abscisa cerrada antes del PT hasta él.

Para tales subcuerdas se puede calcular una deflexión conociendo primero la deflexión correspondiente a una cuerda de un metro (1 m ) de longitud δ_m:

$\frac{{\delta}_m}{1}=\frac{\delta_c}{c}\rightarrow \frac{{\delta}_m}{1}=\frac{G_c/2}{c}\rightarrow {\delta} _m=\frac{G_c}{2c}$

Entonces la deflexión de las subcuerdas se calcula como:

δ_sc = δ_m · Longitud de la subcuerda

La deflexión para el PT, desde el PC, según lo anotado, debe ser igual al la mitad del ángulo de deflexión de la curva:

δ_PT = Δ/2

Lo cual sirve para comprobar la precisión en los cálculos o de la localización en el terreno.

Ejemplo

Para una curva circular simple se tienen los siguientes elementos:

Rumbo de la tangente de entrada: N 76º20′ E
Rumbo de la tangente de salida: N 19º40′ E
Abscisa del punto de intersección de las tangentes, PI: k2+226
Coordenadas del PI: 800 N , 700 E
Cuerda unidad: 20 m
Radio de curvatura: 150 m

Calcular los elementos geométricos de la curva; las abscisas del PC y el PT; las coordenadas del PC, el PT y el centro de la curva; y las deflexiones de la curva.

Solución

Elementos geométricos de la curva

El ángulo de deflexión de la curva está dado por la diferencia de los rumbos de los alineamientos (no siempre es así, en este caso sí porque los dos están en el mismo cuadrante NE):

Δ = 76º20′ – 19º40′ = 56º40′ Izquierda

(A la izquierda porque el rumbo de la tangente de salida es menor que el de la de entrada)

Conociendo el radio y el ángulo de deflexión se pueden calcular los demás elementos geométricos:

Tangente: T = R · Tan (Δ/2)

$T = 150 m \tan\frac{56^\circ 40'}{2} = 80,879 m$

Grado de curvatura: G_c = 2 · Sen^-1[ c / (2R) ]

$G_c=2\arcsin(\frac{20 m}{2(150m)})=7^\circ38^\prime42,39^{\prime\prime}$

Longitud de la curva: L_c = c·Δ/G_c

$L_c = \frac{20 m (56^\circ40^\prime)}{7^\circ38^\prime42,39^{\prime\prime}}=148,243 m$

Cuerda Larga: CL = 2·RSen(Δ/2)

$CL=2(150 m)\sin(\frac{56^\circ40^\prime}{2})=142,380 m$

Externa: E = R(1/Cos(Δ/2) – 1)

$E = 150 m (\frac{1}{\cos(\frac{56^\circ40^\prime}{2})}-1)=20,416 m$

Ordenada Media (Flecha): M = R[1 – Cos(Δ/2)]

$M=150 m (1-\cos\frac{56^\circ40^\prime}{2})=17,970 m$

Deflexión por cuerda: ${\delta}_c=\frac{G_c}{2}$

${\delta}_c=\frac{7^\circ38^\prime42,39^{\prime\prime}}{2} = 3^\circ49^\prime21,2^{\prime\prime}$

Deflexión por metro: ${\delta}_m=\frac{G_c}{2c}$

${\delta}_m=\frac{7^\circ38^\prime42,39^{\prime\prime}}{2(20 m)} = 0^\circ11^\prime28,06^{\prime\prime}/m$

Abscisas del PC y el PT

Conociendo la abscisa del PI y las longitudes, tanto de la tangente (T) como de la curva (L_c):

Abscisa del PC = Abscisa del PI – T
Abscisa del PC = k2 + 226 – 80,879 m = k2 + 145,121

Abscisa del PT = Abscisa del PC + L_c
Abscisa del PT = k2 + 145,121 + 148,243 m = k2 + 293,364

Se debe tener en cuenta que la abscisa del PT se calcula a partir de la del PC y NO del PI, pues la curva acorta distancia respecto a los alineamientos rectos.

Coordenadas de los puntos PC, PT y O

Conociendo los rumbos de las tangentes de entrada y salida se pueden calcular sus azimutes:

Azimut del PC al PI = 76º 20′
Azimut del PI al PC = Contra azimut de PC-PI = 76º 20′ + 180º = 256º 20′
Azimut del PC a O = 256º 20′ + 90º = 346º 20′ (porque el radio es perpendicular a la tangente de entrada en el PC)
Azimut del PI al PT = 19º 40′

Nota: Debe tenerse mucho cuidado con el cálculo de estos azimuts, pues las condiciones particulares de cada curva pueden hacer que cambie la manera de calcularlos. Especialmente el hecho de si el ángulo de deflexión es a la izquierda o a la derecha. Lo que yo recomiendo para no cometer errores es, primero que todo, tener bien claro el concepto de azimut, y luego hacer un dibujo representativo para ubicarse, que sea claro y más o menos a escala.

Recordemos que, conociendo las coordenadas de un punto A (N_A y E_A), las coordenadas de un punto B (N_B y E_B) se calculan a partir de la distancia y el azimut de la linea que une los dos puntos (AB) así:

N_B = N_A + Distancia_AB · Cos(Azimut_AB)
E_B = E_A + Distancia_AB · Sen(Azimut_AB)

Coordenadas del PI:

800N 700E

Coordenadas del PC:

N = 800 + T·Cos(256º 20′) = 800 + 80,879 Cos(256º 20′)

N = 780,890

E = 700 + T·Sen(256º 20′) = 700 + 80,879 Sen(256º 20′)

E = 621,411

Coordenadas del centro de la curva (O):

N = 780,890 + R·Cos(346º20′) = 780,890 + 150 Cos(346º20′)

N = 926,643

E = 621,411 + R·Sen(346º20′) = 621,411 + 150 Sen(346º20′)

E = 585,970

Coordenadas del PT

N = 800 + T·Cos(19º40′) = 800 + 80,879 Cos(19º40′)

N = 876,161

E = 700 + T·Sen(19º40′) = 700 + 80,879 Sen(19º40′)

E = 727,220

Deflexiones de la curva

Para calcular las deflexiones de la curva partimos de las abscisas calculadas para el PC y el PT y dos ángulos que ya están definidos: la deflexión por cuerda y la deflexión por metro.

Como la cuerda unidad es de 20 m quiere decir que las abscisas de la poligonal se vienen marcando a esa distancia, por lo tanto si la abscisa del PC es la k2 + 145,121 , la siguiente abscisa cerrada corresponde a la k2 + 160 (no la k2 + 150 porque no es múltiplo de 20, es decir, si empezamos desde la k0 + 000 sumando de 20 en 20 no llegamos a la k2 + 150 sino a la k2 + 160). Esto genera una subcuerda, cuya longitud se calcula como la diferencia entre las dos abscisas:

Subcuerda de entrada: 2 160 m – 2 145,121 m = 14,879 m

Ahora, si ya se había calculado que por cada metro de curva existe una deflexión δ_m=0º11’28,06», para la primera subcuerda tenemos una deflexión (correspondiente a la abscisa k2 + 160) de:

Deflexión para la abscisa k2 + 160 = 14,879 m * 0º11’28,06» = 2º50’37,64»

A partir de la abscisa k2 + 160 siguen abscisas cerradas cada 20 m (de acuerdo a la longitud de la cuerda unidad), hasta llegar al PC, y la deflexión para cada una de las abscisas siguientes corresponde a la suma de la anterior con la deflexión por cuerda:

Deflexión para la k2+180 = 2º50’37,64» + 3º49’21,2» = 6º39’58.84»
Deflexión para la k2+200 = 6º39’58.84» + 3º49’21,2» = 10º29’20,04»
Deflexión para la k2+220 = 10º29’20,04» + 3º49’21,2» = 14º18’41,24»
Deflexión para la k2+240 = 14º18’41,24» + 3º49’21,2» = 18º08’02,44»
Deflexión para la k2+260 = 18º08’02,44» + 3º49’21,2» = 21º57’23,64»
Deflexión para la k2+280 = 21º57’23,64» + 3º49’21,2» = 25º46’44,84»

Pero ahí hay que parar porque la abscisa del PT es la k2 + 293,364 , por lo tanto se genera otra subcuerda, la de salida, que se calcula de manera similar a la de entrada:

Subcuerda de salida: 2 293,364 m – 2 280 m = 13,364

Y de la misma manera, la deflexión para la subcuerda es de:

Deflexión para la subcuerda de salida = 13,364 m * 0º11’28,06» = 2º33’15,23»

Así que al final, la deflexión para el PT es:

Deflexión para la k2+293,364 = 25º46’44,84» + 2º33’15,23» = 28º20’00,07»

La cual, según lo visto en el artículo, debe corresponder con la mitad del ángulo de deflexión de la curva:

$28^\circ20^\prime00,07^{\prime\prime} \approx \frac{56^\circ40^\prime}{2} = 28^\circ20^\prime$

Con esta información se construye la cartera de deflexiones, que va a ser la que permita materializar la curva en el terreno, pues es la que recibe el topógrafo para hacer su trabajo. A continuación se muestran las tres primeras que debe contener dicha cartera. Las otras tres, hacen referencia a los elementos que ya se calcularon a lo largo de este artículo (es necesario reescribirlos dentro de la cartera), el azimut de los alineamientos rectos (de entrada y salida), y el sentido en el que se deflectará la curva (en este ejemplo desde el PC hasta el PT, que es el sentido en el que aumenta la deflexión). Nótese que la cartera está escrita de abajo hacia arriba, para facilitar el trabajo de los topógrafos.

ESTACIÓN	ABSCISA	DEFLEXIÓN
PT	k2+293,364	28º20’00,07»
	K2+280	25º46’44,84»
	K2+260	21º57’23,64»
	K2+240	18º08’02,44»
	K2+220	14º18’41,24»
	K2+200	10º29’20,04»
	K2+180	6º39’58.84»
	K2+160	2º50’37,64»
PC	k2+145,121	0º00’00»

// // // // // // // // // // // // // // // //

Bibliografía

Cárdenas Grisales, James. Diseño Geométrico de Carreteras. Ecoe ediciones. Bogotá. 2002. Código topográfico de la Biblioteca de la Universidad: 625.7 C266 di

Las ecuaciones mostradas en este artículos están hechas usando $\LaTeX$ en el Interactive Latex Equation Editor de Sitmo, disponible en http://www.sitmo.com/latex

154 Comments

doblevia 14 noviembre, 2007 a las 10:37

@Antonio Peralta: Qué pena por la demora en contestar, no había visto el comentario.
Primero que todo, asumo que la longitud corta de la curva es igual a la cuerda larga de la que habla este artículo. Para calcular su rumbo, conocido el de la tangente de entrada, es necesario recordar que la cuerda larga corresponde a la deflexión hasta el PT. Por lo tanto, esa deflexión es igual a la mitad del ángulo de deflexión completo de la curva (Δ), el cual es el mismo ángulo interno al que te refieres (según los dibujos que aparecen en el post).

Ahora bien, a mi me gusta más trabajar con azimutes en lugar de rumbos. De esa manera, tienes que la dirección de la cuerda larga está dada por el azimut de la tangente de entrada más la mitad del ángulo interno de la curva. Teniendo en cuenta que ese último ángulo es positivo o negativo, según si la curva es a la derecha o a la izquierda. Finalmente, el resultado lo conviertes nuevamente a rumbo y tienes tu respuesta.

Si no recuerdas bien cómo convertir entre rumbos y azimutes, te recomiendo que leas este post:
https://doblevia.wordpress.com/2007/07/25/direccion-de-una-linea-rumbo-y-azimut/

Responder
Pedro 14 noviembre, 2007 a las 09:40

Queria felicitarlos por tan excelente pagina, me ha sido de gran ayuda todas las cosas que he encontre aqui, los temas estan muy bien explicados de una forma clara y sencilla, de verdad muchas felicitaciones, y gracias por colaborarnos con nuestros estudios.

Responder
Antonio Peralta 29 octubre, 2007 a las 12:33

Muy interesante el desarrollo del problema.
Les pido un gran favor: necesito saber como encontrar el rumbo de la longitud corta de una curva circular simetrica, si los unicos datos que tengo son: el rumbo de la tangente de entrada y el angulo interno de la curva.

Responder
Enzo 22 octubre, 2007 a las 12:35

uy!
muchas gracias, me ayudaste muchisimo! 😀
y pues si te demoraste en contestar un poco realmente le diste en el clavo y muchas gracia spor la ayuda eso era lo q queria saber 😀
tengo otra duda, no se si podras postearala porfa!
necesito una «guia» de como construir una curva de transicion, y cuales son los elementos básicos q debo hallar, tengo una pero me pide demasiados elementos y se hace toda una telaraña q a una gran escala se hace imposible definir….
luego quiesiera saber cual seria la distancia mínima que debería haber entre una curva compuesta inversa, segun una norma fije 30 m, pero no se si vaya a ser correcto, me dijeron q la distancia no importa, que la transicion del peralte se realiza inclusive si no existe distancia entre estas curvas inversas, es cierto esto?
muchas gracias por la ayuda! :D:D:D
PD: sry por la palabra fuerte, estsba desesperado a las 3 de la mañana con esta duda y no sabia a quien acudir y me sentia un poco frustrado xD

Responder
doblevia 22 octubre, 2007 a las 12:00

@Enzo: Primero que todo te pido disculpas por la demora en contestar. Pero es que he tenido dificultades para entender cuál es exactamente el problema. Lo he leído en varias ocasiones y lo he discutido con mis compañeros. Así que no sé si le pegué a lo que preguntas:

Para empezar, en Colombia no utilizamos el término «progresivas». Supongo entonces que se refiere a las abscisas, es decir, el kilometraje que marca el eje de la vía a partir de un punto de referencia.

Ahora, lo que entiendo del problema es que tienes una primera curva, de la que conoces las abscisas (progresivas) del PC, el PI y el PT; pero no tienes sus elementos (T, R, Lc, M, E, etc.). Luego tienes otra curva, que sigue a la anterior. De la cual conoces sus elementos, pero no sus abscisas (progresivas). Adicionalmente, tienes la distancia entre los PI de cada curva. El problema radica en conocer las abscisas de la segunda, ¿cierto?.

Entonces, de la primera curva puedes obtener el valor de su tangente (T1) a partir de las abscisas que conoces. Pues está dada por la del PI menos la del PC:
T = PI – PC
Como tu lo mencionas, hay que tener cuidado de no hacerlo con el PT menos el PI, debido al «error de curvatura», que no es un error, sino una propiedad: la curva recorta camino respecto a los trazos rectos.

Como la tangente de una curva circular simple es la misma tanto a la entrada como a la salida, y conoces la tangente de la segunda curva, puedes calcular la entretangencia, es decir, la distancia entre el PT1 y el PC2. Tal longitud está dada por la siguiente expresión:
EntreTangencia = Distancia entre PI’s – (T1+T2)

Ahora, esa distancia de entretangencia se le suma a la abscisa (progresiva) del PT1 y obtienes la correspondiente abscisa del PC de la segunda curva. Luego le sumas la longitud de la curva y tienes como resultado el PT.

Espero haber sido de ayuda 🙂

La próxima vez no te desesperes y haz un dibujo que te pueda ayudar a entender mejor la situación. Y, por favor, trata de no poner palabras fuertes en tus comentarios.

Hasta pronto.

Responder
Enzo 10 octubre, 2007 a las 00:34

quisiera saber como podria encontrar las progresivas de una carretera con curvas simples, tomando en cuenta q tienes como dato el angulo, T, Lc, M, E, y tambien tienes como dato el primer PC y el primer PT y el primer PI, y tambien tengo los datos de las distancias entre cada PI, pero no puedo usar estos ultimos datos para hallar los PC’s y los PT’s ya q existiria una error por curvatura, q metodo puedo usar o q formula q no sea con coordenadas, sino con progresivas, para poder hallar las demás PC’s y PT’s?
tengo mas o menos una idea de hallar el PI como el PC menos la mitad de la longitud de la curva pero tendria q sumarla a la distancia entre el siguiente PC menos el PT anterior mas la suma de la longitud de curva siguiente, pero como mierda hallo esa distancia? :S ayuda por favor!

Responder
Daniel 6 septiembre, 2007 a las 21:00

wey que bien te quedo la página y son útiles las definiciones!

Responder
Curvas Espirales de Transición « Doble Vía · Ingeniería Civil 3 septiembre, 2007 a las 23:48

[…] que nos van a ayudar más adelante: Curvatura: Se entiende como el inverso del radio de la curva circular. En recta la curvatura es cero porque el radio se hace infinito, mientras que para una curva de […]

Responder
doblevia 26 agosto, 2007 a las 16:19

@Javier: El radio de curvatura se puede calcular si se conoce la longitud de la tangente y el ángulo de deflexión, utilizando la fórmula que aparece en el artículo (y que vimos en clase). Esta es una buena opción para controlar el traslapo de curvas cuando los tramos rectos son muy cortos.
De todos modos, el método más empleado es escoger un radio mínimo de diseño en función de la velocidad específica y, a partir de allí aumentarlo según lo crea conveniente el diseñador. Para tal efecto se puede uno valer de las tablas que aparecen en el Manual de Diseño Geométrico para Carreteras del INVIAS. En este archivo aparecen el radio y el peralte (esto lo vemos después) en función de la velocidad específica interpolada cada 1 km/h.

Responder
Javier Barrios 26 agosto, 2007 a las 15:50

Edgar,
¿como se halla o se obtiene el radio de curvatura? Tengo duda si sale por alguna tabla o por formula. Dependiendo, por favor enviar la información.
Gracias

Responder
doblevia 16 agosto, 2007 a las 19:45

@Sebas: Lamento no poder ayudarte como quisiera, pero los pavimentos no son mi fuerte. Sin embargo, averiguando por ahí, sé que el BPR viene de Bureau of Public Roadas y que efectivamente tienen un método para medir la rugosidad en los pavimentos. Puedes intentar una búsqueda en google (o cualquier otro buscador) de los siguientes términos: «bpr roughometer»; es mejor en inglés porque generalmente se encuentra más información sobre ingeniería en ese idioma, más aún cuando se trata de una entidad de los Estados Unidos.

Responder
Sebas 15 agosto, 2007 a las 05:53

..hola como estas, mira quisera saber si tenes algo respecto a DEFLEXION para el calculo de BPR…resultan de la medicion que realiza un equipo que mide la rugocidad del camino…no tengo mas datos tan solo esa informacion…muchas gracias desde ya.-

Responder
doblevia 27 julio, 2007 a las 10:22

@Simeon: Según te entiendo te refieres a la diferencia en la localización del PT cuando se materializa por la curva (siguiendo las cuerdas y subcuerdas) y cuando se ubica desde el PI (midiendo la tangente, T).
Es lógico que los dos puntos no van a coincidir en el terreno (a pesar de que en el diseño sí lo hacen) porque han sido trazados de manera diferente y en el campo no puedes medir con la precisión que diseñas (debido a las aproximaciones de los aparatos). En Colombia aceptamos como válido un error de cierre, en longitud, equivalente a 1 cm por cada cuerda y subcuerda que se haya medido; el error angular admisible corresponde a la aproximación del aparato (teodolito, tránsito, estación, etc.) igualmente por cada cuerda y subcuerda subtendida.
Por ejemplo, para el ejercicio del post se tienen dos subcuerdas (una a la entrada entre el PC y el k2+160 y otra entre el k2+280 y el PT) y 6 cuerdas (de 20 m ). Por lo tanto, la máxima diferencia que debe existir entre el PT materializado desde el PI y el que sale del último punto localizado con las deflexiones será:
En longitud: 1 cm * 8 cuerdas y subcuerdas = 8 cm
En ángulo (suponiendo que la curva se traza con un teodolito de aproximación a los 10″): 10″ * 8 cuerdas y subcuerdas = 80″ = 0º01’20»
Existen otros parámetros para definir cuál puede ser el desfase máximo, pero no los tengo a mano en este momento. Voy a averiguarlos y luego los pongo en otro comentario 😉 También los puedes buscar en el libro: Diseño de Carreteras: Técnicas y Análisis del Proyecto de Paulo Emilio Bravo.
PD: Simeon: Trata de mejorar tu ortografía 🙂

Responder
simeon 26 julio, 2007 a las 19:58

los trasos son fasinantes, ma que nada los calculos pero si no te consentras puedes fracasar en el trazo, tenga mas precaucion.

Responder
simeon 26 julio, 2007 a las 19:46

habiendo buscado encontre algunas formulas que se utiliza en el diseño de curvas horizontales, solo quiero saber como debe quedar el trazo con las progresivas y el PI, debe concordar las medidas con la progresiva del PI o puede desfasarse quiero por favor que me expliques

Responder
doblevia 1 junio, 2007 a las 16:57

@Leticia: Yo no sé cómo! El grado de curvatura define que tan “cerrada” es una curva y es una función directa del radio, es decir, curvas con diferentes radios tienen diferentes grados de curvatura para la misma cuerda (o arco) unidad, así tengan el mismo ángulo de deflexión. Para que quede más claro te pongo esta gráfica.
La única opción que yo veo es que despejes el radio de alguna otra fórmula, por ejemplo dejarlo en función del delta y la tangente, pero igualmente lleva implícito el radio, además dices que sin despejar. 😦

Responder
leticia 29 May, 2007 a las 13:54

quiero saber como se calcula el grado de curvatura, si no se tiene el radio y sin despejar las formulas.

Responder
doblevia 9 May, 2007 a las 11:21

@José Antonio: Gracias. Es cierto que faltan esos temas, pero ten en cuenta que este post es únicamente sobre curvas circulares simples. Espero publicar el mes entrante otros temas como los que tu dices.

Responder
jose antonio marquez vazquez 8 May, 2007 a las 17:05

la exposicion de los elementos es entendible pero le falta otros elementos como o porque seligan a curvas de transisicon como se calcula sobre ancho de la curva y la sobrelevacion (peralte) espero que puedan ampliar esta información

Responder
doblevia 6 May, 2007 a las 15:17

@Juan M: Muchas gracias por tu comentario. El diagrama de masas para una carretera lo vamos a ver esta semana con mis estudiantes, pero por ahora no tengo preparado el post para ponerlo en esta página, lo siento. Por ahora te puedo dar como referencia estos dos libros que hablan un poco del tema:

Chocontá Rojas, Pedro Antonio. Diseño Geométrico de Vías. Editorial Escuela Colombiana de Ingeniería. Bogotá. 1998.
McCormac, Jack. Topografía. Limusa Wiley. 2005.

Además buscando por ahí en internet puedes encontrar mucha más información.

Responder
juan martinez 5 May, 2007 a las 21:31

esta muy bien esta pagina, pero queria saber si no tendran textos sobre curva masa de terracerias de un camino, es para un trabajo…se los agradeceria mucho.gracias

Responder
doblevia 3 May, 2007 a las 19:43

@Juan: Lamentablemente no tengo información sobre proyectos de túneles, pero tal vez en la página del Instituto Nacional de Vías –INVIAS– (yo he tenido problemas para ingresar últimamente) y consultar sobre el proyecto del túnel de la línea. Lo siento

Responder
juan zebalos 3 May, 2007 a las 12:42

un favor no pueden poner algo sobre proyectos de tuneles es para una tesis les agradeceria mucho

Responder
doblevia 3 May, 2007 a las 09:33

@Benajmín, William y Sara: Muchas gracias 😉

@Sara: Tienes razón, el cálculo de las coordenadas cambia si la curva es hacia la izquierda (ángulo de deflexión negativo), vale la pena hacer la salvedad. Aunque yo pienso que para evitar confusiones lo más fácil es realizar un dibujo a mano alzada aproximado de la situación y ubicarte mejor.

Responder
1. WANA 2 julio, 2013 a las 21:33
  
  CLARO SIEMPRE HAY QUE TENER EN CUENTA LOS AZIMUT DE ENTRADA DEL PC AL PI U UBICARTE EN EL CUADRANTE SI HACES ESO MAL DESDE EL INICIO ESTAS PERDIDIO TODO LOO QUE CALCULES ESTARIA MAL
  
  Responder
Sara 2 May, 2007 a las 21:44

Hola me parece muy buena esta pagina, realmente he aclarado muchas dudas pero creo que deberia haber algunos ejemplos donde el angulo de deflexion sea negativo ya que asi cambian las formulas para el calculo de coordenadas. gracias

Responder
wiliam 25 abril, 2007 a las 18:50

me parecio bien .los graficos podrian mejorarlos con ilustraciones de campo.gracias

Responder
benjamin 16 abril, 2007 a las 09:01

muchas grcias me aclararon todas mis dudas y me ayudo para mi informe chao (chile)

Responder
doblevia 15 abril, 2007 a las 17:46

@Esteban: Muy buena idea, lo que pasa es que el ejercicio de ejemplo no està terminado, falta la cartera de las deflexiones de la curva y bien podrìa estar acompañado de unas gràficas. Dàme un tiempo y las harè. La cosa es que no he querido simplemente escanear las que aparecen en los libros por cuestiones de derechos de autor 😉

@agus: Me parece que el càlculo de áreas por coordenadas es más un tema de topografía y ya lo vimos en clase con mis alumnos, se me hizo un tanto sencillo y por eso no lo he puesto en el blog, pero a tu pedido voy a ver si por lo menos la explicación la publico, per búscalo bajo la categoría asignaruras/topografía

Responder
1. Katia 24 May, 2013 a las 14:45
  
  Necesito bibliografía digital sobre diseño geométrico y estructural en vías férreas.
  Ayuda por favor
  
  Responder
agus 15 abril, 2007 a las 17:39

seria bueno que pusieran mas del como calcular la superficie de un terreno mediante el metodo VIA COORDENADAD y asi usar unos ejemplos para una mejor comprencion

Responder
Esteban de jesus Moreno E 12 abril, 2007 a las 17:36

Muy bueno y clara su explicacion del calculo de la curva, pero podria atravez de unos graficos, explicar el proceso en el campo.
gracias

Responder
1. emelina peña 27 diciembre, 2009 a las 14:55
  
  por favor manadr ejercicios de curvas simples gracias para haber si entendi mucchas gracias
  
  Responder
2. WANA 2 julio, 2013 a las 21:25
  
  SOY INGENIERO GEODESTA DE LA UNIVERSIDAD AUTONOMA DE SINALOA MEXICO PARA EVITARNOS TANTA FARAMALLA EN CAMPO HACEMOS VER LAS CURVAS CIRCULARE, ESPIRALES Y VERTICALES MAS FACIL DE CALCULAR DE LO K KRES Y RAPIDAS
  
  Responder
  1. kevin 16 noviembre, 2013 a las 11:23
    
    me puedes hacer favor de mandarme algo para calcular una curva horizontal y vertical mas simple gracias..