Una manera de describir los accidentes, la forma y los detalles de un terreno (de lo que se encarga la topografía) consiste en realizar un levantamiento utilizando líneas rectas que forman un polígono, ya sea abierto o cerrado, mediante la medición de distancias y ángulos, y a partir de él tomar los detalles que sean necesarios.
La dirección de una línea no es más que el ángulo horizontal que ésta forma con una línea de referencia, llamada meridiano de referencia, que -como ya se vio en otro artículo– puede ser un meridiano magnético, geográfico o arbitrario.
El ángulo medido a partir de esa referencia, que designa la dirección de la línea, puede ser un Rumbo o un Azimut, de cuya descripción y cálculos se tratará enseguida.
Rumbo
El rumbo de una línea es el ángulo horizontal agudo (<90°) que forma con un meridiano de referencia, generalmente se toma como tal una línea Norte-Sur que puede estar definida por el N geográfico o el N magnético (si no se dispone de información sobre ninguno de los dos se suele trabajar con un meridiano, o línea de Norte arbitraria).
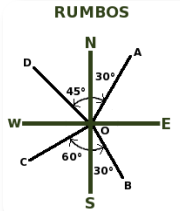
Para determinar el rumbo de una línea es necesario conocer la ubicación de la línea de referencia desde la estación (punto de medida). En el caso de la figura de la izquierda se supone que existe un instrumento localizado en el punto O (estación), desde el cual se puede observar la línea Norte – Sur (NS) y configurar una cruz que señala los cuatro puntos cardinales. Luego se da vista al segundo punto que conforma la línea, para el ejemplo van a ser cuatro: A, B, C y D.
Como se observa en la figura, los rumbos se miden desde el Norte (línea ON) o desde el Sur (línea OS), en el sentido de las manecillas del reloj si la línea a la que se le desea conocer el rumbo se encuentra sobre el cuadrante NOE o el SOW; o en el sentido contrario si corresponde al cuadrante NOW o al SOE.
Como el ángulo que se mide en los rumbos es menor que 90° debe especificarse a qué cuadrante corresponde cada rumbo. Por ejemplo, las líneas mostradas tienen los siguientes rumbos:
| LÍNEA | RUMBO |
| OA | N 30° E |
| OB | S 30° E |
| OC | S 60° W |
| OD | N 45° W |
Como se puede observar, en la notación del rumbo se escribe primero la componente N o S del cuadrante, seguida de la amplitud del ángulo y por último la componente E o W.
Rumbo inverso (también conocido como contra-rumbo)
En el ejemplo de la figura anterior todos los rumbos se midieron desde el punto O. Cuando se trata del rumbo de la misma línea, pero observado desde el extremo opuesto se habla de rumbo inverso o contra-rumbo. Convertir rumbos a contra-rumbos es muy sencillo, pues los ángulos son ángulos alternos-internos (recordar el teorema de ángulos congruentes en una secante que corta dos líneas paralelas), entonces el único trabajo que resta es cambiar las letras que indican el cuadrante por las contrarias, es decir N por S (y viceversa) y E por W (y viceversa).
Con la misma figura de antes se tienen los siguientes rumbos inversos:
| LÍNEA | RUMBO |
| AO | S 30° W |
| BO | N 30° W |
| CO | N 60° E |
| DO | S 45° E |
Para resumir:
| LÍNEA | RUMBO | CONTRA-RUMBO |
| OA | N 30° E | S 30° W |
| OB | S 30° E | N 30° W |
| OC | S 60° W | N 60° E |
| OD | N 45° W | S 45° E |
:-
Azimut
El azimut (o acimut; ambas grafías son válidas de acuerdo a la RAE) de una línea es el ángulo horizontal medido en el sentido de las manecillas del reloj a partir de un meridiano de referencia. Lo más usual es medir el azimut desde el Norte (sea verdadero, magnético o arbitrario), pero en ocasiones se usa el Sur como referencia.
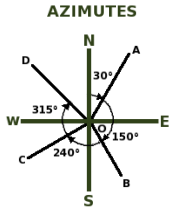 Los azimutes varían desde 0° hasta 360° y no se requiere indicar el cuadrante que ocupa la línea observada.
Los azimutes varían desde 0° hasta 360° y no se requiere indicar el cuadrante que ocupa la línea observada.
Al igual que con los rumbos es necesario conocer primero la ubicación del meridiano Norte – Sur de referencia y luego apuntar la visual hacia el punto final de la línea que se va a medir. Para el caso de la figura mostrada a la izquierda, las mismas líneas para las que se había encontrado el rumbo tienen el siguiente azimut:
| LÍNEA | AZIMUT |
| AO | 30° |
| BO | 150° |
| CO | 240° |
| DO | 315° |
Azimut inverso (también conocido como contra-azimut)
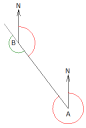 De la misma manera que con los rumbos, si se mide el azimut de una línea desde el extremo opuesto al inicial se está midiendo el azimut inverso. El contra-azimut se calcula sumándole 180° al original si éste es menor o igual a 180°, o restándole los 180° en caso de ser mayor.
De la misma manera que con los rumbos, si se mide el azimut de una línea desde el extremo opuesto al inicial se está midiendo el azimut inverso. El contra-azimut se calcula sumándole 180° al original si éste es menor o igual a 180°, o restándole los 180° en caso de ser mayor.
En la figura de la izquierda se puede ver cómo, si se le restan 180º (ángulo recto en verde) al azimut de la línea AB se obtiene su contra-azimut, es decir el azimut de la línea BA. De igual forma, si los 180º se suman al azimut de BA se obtiene el de AB. Entonces:
Para la figura mostrada anteriormente se observan los siguientes azimutes inversos:
| LÍNEA | AZIMUT | CONTRA-AZIMUT |
| OA | 30° | 30°+180° = 210° |
| OB | 150° | 150°+180° = 330° |
| OC | 240° | 240°-180° = 60° |
| OD | 315° | 315°-180° = 135° |
Vale la pena volver a decir que en ningún caso un rumbo (o un rumbo inverso) puede ser mayor a 90°, ni un azimut (o contra-azimut) mayor a 360°.
Conversiones
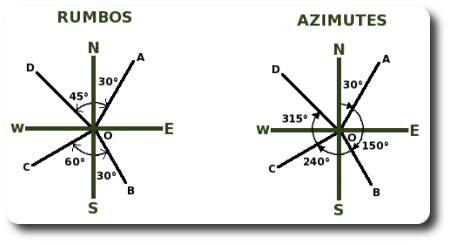
De rumbo a azimut
Para calcular azimutes a partir de rumbos es necesario tener en cuenta el cuadrante en el que se encuentra la línea. Observando la figura anterior se puede deducir la siguiente tabla:
| Cuadrante | Azimut a partir del rumbo |
| NE | Igual al rumbo (sin las letras) |
| SE | 180° – Rumbo |
| SW | 180° + Rumbo |
| NW | 360° – Rumbo |
Se puede comprobar revisando los valores que aparecen en la figura de arriba.
De azimut a rumbo
Observando también la figura se ve que el cuadrante de la línea depende del valor del azimut así:
| Azimut | Cuadrante | Rumbo |
| 0° – 90° | NE | N ‘Azimut’ E |
| 90° – 180° | SE | S ‘180° – Azimut’ E |
| 180° – 270° | SW | S ‘Azimut – 180°’ W |
| 270° – 360° | NW | N ‘360° – Azimut’ W |
:-
Cálculo de Azimutes en poligonales
 Una poligonal, sea abierta o cerrada, es una sucesión de distancias y direcciones (rumbo o azimut) formadas por la unión de los puntos en los que se armó el instrumento que se usó para medirlas (puntos de estación). Cuando se ubica el instrumento en una estación se puede medir directamente el azimut de la siguiente línea a levantar (si se conoce la dirección del N o si se «sostiene» el contra-azimut de la línea anterior), sin embargo, en ocasiones se mide el ángulo correspondiente entre las dos líneas que se intersectan en el punto de estación (marcando «ceros» en el ángulo horizontal del instrumento cuando se mira al punto anterior), a este último ángulo se le va a llamar «ángulo observado».
Una poligonal, sea abierta o cerrada, es una sucesión de distancias y direcciones (rumbo o azimut) formadas por la unión de los puntos en los que se armó el instrumento que se usó para medirlas (puntos de estación). Cuando se ubica el instrumento en una estación se puede medir directamente el azimut de la siguiente línea a levantar (si se conoce la dirección del N o si se «sostiene» el contra-azimut de la línea anterior), sin embargo, en ocasiones se mide el ángulo correspondiente entre las dos líneas que se intersectan en el punto de estación (marcando «ceros» en el ángulo horizontal del instrumento cuando se mira al punto anterior), a este último ángulo se le va a llamar «ángulo observado».
Si el ángulo observado se mide hacia la derecha (en el sentido de las manecillas del reloj, que es el mismo en el que se miden los azimutes) se puede calcular el azimut de la siguiente línea con la siguiente expresión:
Azimut línea siguiente = Contra-azimut de la línea anterior + Ángulo observado
Se debe aclarar que si el resultado es mayor a 360° simplemente se le resta este valor.
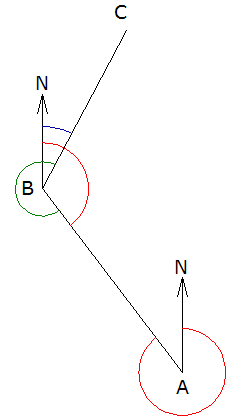
En la figura se observa que si el azimut conocido corresponde al de la línea AB (ángulo NAB en rojo), por lo tanto el contra-azimut es el ángulo NBA (también en rojo). El ángulo observado, medido en el sentido de las manecillas del reloj con el instrumento estacionado en el punto B es el ángulo ABC (en verde). El azimut que se desea conocer es el de la línea BC (ángulo NBC en azul). Por lo tanto se tiene la siguiente expresión:
Azimut BC = Contra-Azimut AB + Ángulo observado en B
Azimut BC = <NBA + <ABC
Como es evidente que el resultado será mayor que 360° (en este caso en particular) entonces el azimut de la línea BC será:
Azimut BC = (<NBA + <ABC) – 360°
Esta expresión es válida sólo si el ángulo observado está medido en el mismo sentido del azimut (derecha), sin importar si es interno o externo.
Si se trata de calcular rumbos se pueden luego convertir los azimutes calculados de la forma anterior.
/ / / / / / / / / / / / / / / / / / / /
Bibliografía
Paul R. Wolf y Russel C. Brinker. Topografía. Novena Edición. Alfaomega. México, 1997

oye tengo una duda… soy estudiante de ing. civil en la universidad veracruzana en mexico.. pero quisiera saber si no puesdes colocar las formulas para encontrar los azimut y distancias del poligono… creo q es mediante un formula mas omenos asi Pol(x2-x1,y2-y1),,, no recuerdo pero sime ayudas te lo agradeceria
La distancia horizontal es igual a= √(E2-E1)+(N2-N1) donde E y N son norte y este o si son coordenadas cartecianas Este seria el eje X y Norte seria eje Y y la formula seria así:
√(X2-X1)+(Y2-Y1)
El azimut depende del cuadrante si es NE seria el mismo rumbo si es SE seria 180-rumbo si es SW es 180+rumbo si es NW es 360-rumbo. Espero q te ayude ..
Las componentes e la distancia son al cuadrado
Hay una formula en excel para calcular azimut de una poligonal
hola soy estudiante de ing. en construcción exelente tu material gracias me ayudo mucho para resolver muchas dudas.
de antemano te felicito.
Hola los comentarios que hace doblevia son bastante buenos en lo que se refiere en azimuts y rumbos, me gustaria saber si conoses algun Software que calcule el azimut de una linea atravez de astronomia de posición.
hola necesito urgentementa las formulas topograficas como son la formula general de la altimetria, planimetria, calculo de rumbos y acimutes, poligonales abiertas y cerradas, curvas de nivel, levantamientos para una construccion y sus respectivas formulas de los agradecere muchisimo¡¡¡¡¡¡¡¡¡¡
@ Miguel Angel: A partir de las coordenadas de los puntos 125 y 127 puedes conocer el rumbo de la línea que los une. Si haces un dibujo de los dos puntos, te das cuenta de que se puede formar un triángulo rectángulo, cuya hipotenusa es la línea en cuestión, mientras que los catetos están definidos por las proyecciones Este y Norte de dicha línea. Entonces, el rumbo está determinado por la arcotangente de la diferencia de las coordenadas Este, sobre la diferencia de las coordenadas Norte así:
Rumbo = Atan((E127 – E125)/(N127 – N125))
Desde luego, debes tener en cuenta en qué cuadrante se encuentra la línea. Una vez tengas el rumbo, lo puedes convertir a azimut como indica el post.
Cuando tengas el azimut de la línea 125-127, conocidas las coordenadas del punto 125, revisa el comentario 19 de esta misma página.
hola… mira estuve biendo tu pagina y esta muy interezante y presisamente tengo un problema
mira tengo mi teodolito en en el punto 125 y estoy visando el 127 ambos con sus coordenadas correspondientes (x,y) y quiero poner un punto auxiliar a 34.567m y giro a un angulo de 57º20´40″ como se que coordenadas tiene ese punto o la formula para hacerla… bueno espero me puedas ayudar gracias…
La formula es
x mas distancia × seno del acimut igual a x .
y mas distancia × coseno del acimut igual a y
estoy buscando el calculo de azimut y distancia a partie de coordenadas, para ver en que me prodias ayudar
Hola, antes que nada le envio un cordial saludo, soy nuevo en estas cuestiones y queria saber si existe algun programa o formula para poder convertir rumbos magneticos de un predio a coordenadas geograficas o a coordenadas UTM, y si existiera me pudieran indicar como conseguirlo.
Gracias
@ William alberto: Muchas gracias. Por favor mira el comentario 4 de esta misma entrada para resolver tu duda.
@ Gilberto Ramos: Hola. Si entiendo bien tu pregunta, es similar a la de Harold (un par de comentarios antes que el tuyo). Sólo debes repetir el procedimiento para cada vértice hasta volver al primero.
Hola, quisiera saber como sacar los demas vertices de un Poligono. En mi caso tengo un poligona de 5 lados diferente distancia. Cuento con los rumbos y con un vertice. Todo esta en coordenadas geograficas, lo que requiero es una formula. Lo de los rumbos y azimutes me queda muy claro.
Gracias
Hola, felicitaciones ante todo por esta increible pagina, quisiera que alguno de ustedes me facilitara la formula matematica para el calculo de un azimut a partir de las coordenadas conocidas. muchisimas gracias y reitero mis felicitaciones, espero tener mucho contacto con ustedes.chao
@ Harold Avenia: ¡Hola! Siento mucho la demora en contestar, pero he estado un poco ocupado estos días.
Cuando tienes las coordenadas de dos puntos, la línea que los une forma un triángulo rectángulo, cuyos catetos son la proyección Norte y la proyección Este de la línea (que es la hipotenusa). A su vez, el azimut se puede convertir en uno de los ángulos agudos del triángulo. De manera que las proyecciones se pueden calcular de manera similar a las componentes de un vector.
Ahora bien, si conoces las proyecciones, puedes ir de un punto a otro «caminando» sobre ellas. Es decir, desde el punto 1 puedes conocer las coordenadas del punto 2. Con ello, puedes obtener las siguientes fórmulas (siendo a el punto conocido y b el desconocido):
N_b = N_a + ProyecciónN_ab
N_b = N_a + Distancia_ab*Coseno(Azimut_ab)
E_b = E_a + ProyecciónE_ab
E_b = E_a + Distancia_ab*Seno(Azimut_ab)
De manera que, para el problema que tu tienes, la cosa sería así (asumo que el punto conocido se llama a, que x es la coordenada Este e y la coordenada Norte):
N_b = y + D*Cos(A)
N_b = 10,971 5 + 853,818 679*Cos(37,721 618)
N_b = 686,335 88
E_b = x + D*Sen(A)
E_b = -74,820 4 + 853,818 679*Sen(37,721 618)
E_b = 447,567 66
Finalmente, una pregunta: ¿por qué usas tantos decimales (especialmente para las distancias)?
hola doble via…
mira tengo una cuestion y estoy un poco enredado necesito encontrar una coordenaga geografica de un punto de acuerdo un punto de referencia geograficamente conocido junto con el azimut (angulo) y la distancia que recorre al punto en esa dirreccion.. bueno no se como sacar dicho punto cuando son coordenadas geograficas…
eje:
punto conocido x=-74.8204 y=10.9715
Azimut A= 37.721618
Distancia D= 853.818679
desearia saber como puedo la coodenada geografica del segundo punto….
wow!! super wow!! esto esta genial me sacaste de un apuro en mi tarea
papa!!
Tus explicaciones me han parecido muy claras, y he querido compartir con mis estudiantes tus conceptos, por tal razón te enlace en el blog.
gracias
me podrias amigho aclarar como explico un pt inaccesible,debo de saberlo y como vencerlo en el campò con un aparato simple ,ya sea transito.
buenas,mira solo queria aclarar la duda del joven que pregunta el modo de calculo de distancias y azimutes en calculadoras corrientes,supongo que te referis ala cientifica.es muy simple:tenes las cooredenas.le das polares(pol) y le le metes la dieferencia de nortes,le das coma y le metes la diferencia de estes.entonces primero te arroja la distancia horizontal,le das alfa f y te vota rumbo o azimut,segun el cuadrante.
@ Isis: Por favor mira el artículo que aparece en la siguiente dirección:
https://doblevia.wordpress.com/2007/02/06/el-valor-mas-probable/
kiero esa definicion por favor q es un error probable 🙂
ten horas buscando la definicion de q error probable, para la materia de matematicas aplicada. si tienen algo pues facilitenmelo por favor gracias. bye
@ Marco: Gracias por tu comentario. No sé a qué te refieres con fórmulas para una calculadora corriente. No veo que haya ninguna que requiera de un procesamiento o cómputo complicado. Hace poco revisé algunos exámenes de mis estudiantes utilizando la calculadora de mi celular. Aquí sólo hay sumas y restas. ¡Ah! Y mucho cuidado, es decir, realizar los cálculos con precaución para no cometer errores tontos. 😀
@ CTRL-ALT-SUP: Muchísimas gracias 🙂
@ Gerardo: Gracias. A mi también me gustaría que hubieran más ejemplos. Tengo que aprovechar mejor el tiempo para poner más posts. He estado un poco alejado del blog. Lo siento.
De todos modos, muchas gracias a tod@s por comentar.
esta muy bien, me gustaria que hubiera mas ejemplos para calcular las poligonales, tanto en azimutes y rumbos
Muy bueno el articulo, ademas con las explicaciones en imagenes me ayudo mucho, y eso que apenas me lo enseñaron aqui en el CETIS 134, PERO MUY BUENO, GRACIAS Y SALUDOS DESDE MEXICO.
Esta reweno , pero sabes me gustaría saber la formula para el calculo de azimut y distancia para calculadoras cientificas corrientes , seria genial si te supieras alguna . bueno saludos……
Hay un libro del ingeniero Guerra Bustamante «Trazo y diseño de carreteras, ferrocarriles y Canales» Que cada capitulo termina con un programa para calculadora cientificas quizas te pueda servir
Saludos
@ Juanita: Muchas gracias. Me alegra que te hayan servido. :d Una pregunta: ¿tu apellido es Melgar? Es curioso porque yo pasé buena parte de mi infancia en un pueblo que se llama así. ¡Saludos en Argentina!
Muy claras las explicaciones, te felicito
@Lariux: La fórmula sale de poner en un dibujo las coordenadas que tienes y trazar la línea que une los puntos que tienes. Como los ejes de las coordenadas Nortes y Estes son perpendiculares, te das cuenta de que puedes armar un triángulo rectángulo.
Si estas parada en el punto GPS1 y visas al punto GPS2, que está más al N y al E, el ángulo del triángulo en cuestión, que tiene vértice en GPS2, tiene la siguiente tangente:
Tan(GPS2) = (X2-X1) / (Y2-Y1) = (XGPS2 – XGPS1) / (YGPS2 – YGPS1)
Por lo tanto dicho ángulo está dado por la arcotangente (tan^-1) de la división entre la diferencia de las coordenadas Este y la diferencia de las coordenadas Norte. Ese ángulo, por alternos internos (siguiendo los teoremas de ángulos en líneas paralelas cortadas por una secante), es equivalente al azimut de la línea GPS1-GPS2.
Luego de que tienes el azimut te queda más fácil convertirlo a rumbo siguiendo las indicaciones dadas en este artículo.
😉
si tengo las coordenadas de un par de gps
GPS 1 x=2168607.266 y=475317.761
GPS 2 x=2168852.053 y=475581.302
y quiero calcular el azimut de inicio y el rumbo que debo de hacer para saber cual es XY2 y cual XY1 ya vez que la formula es la siguiente
(X2-X1)/(Y2-Y1) TAN-1
ESTOY PARADO EN EL GPS1 Y VISO A GPS2
para empesar tus coordenadas estan invertidas tu estas en la zona 14Q NORTE UTM en lomas del bosque a un costado de la autopista chamapa lecheria. la distancia entre estos dos puntos visando gps1 a gps 2 es de 359.68 mts. de acuerdo a la formula de hipotenusa h2=x2+y2; y el rumbo 38ª59’22.23″
coreccion el rumbo aso como el azimut el igual a (X2-X1)/(Y2-Y1)TAN^1
RBO N47º06’46.38″E Y EL AZIMUT ES IGUAL SOLO QUE SIN LETRAS POR ESTAR EN EL PRIMER CUADRANTE.
Hola,
Pero que pasa si poseo coordenadas geográficas (con hora, minutos y segundos) y deseo obtener el rumbo, y distancia?
Las coordenadas por ej. GPS 1 no es igual a coordenadas con latitud y longitud geográfica.
@Julián: Gracias por el comentario. Estoy re-leyendo el artículo para ver qué se puede mejorar. Te recomiendo que antes de leer este artículo hayas leido ya esta introducción.
De todos modos, si tienes alguna pregunta específica, no dudes en hacerla. 😀
hola soy estudiante de topografia de la ubiversidad distrital y no se entiende nada del articulo, podrianser mas claros y especificar bein los terminos.
gracias de antemano
Salgase de esa carrera qe es mala .|.
Ah bueno!!!
marys.. yo soy ingeniero topografo, estudie en la Universidad de Guadalajara en jalisco Mexico, no es una carrera mala, es una carrera emocionante que nunca te va a dejar detras de un escritorio, al contrario, cada dia es diferente y siempre te lleva a conocer lugares que normalmente y en otras situaciones.. quizas nunca conoceria, la topografia es la base de todas las carreras, va de la mano de la fisica y matematicas y siempre acompañada de una nueva aventura.. saludos marys
Jajaj el comentario patetico de alguna secretaria mal asalariada.
SORRY PERO ESTAS COMPLETAMENTE EQUIVOCADA PRECIOSA . . . SALUDOS
UNIVERSIDAD !!!
mmmm soy estudiante de ingenieria geofisica en el insituto politecnico nacional (mexico) creo que esta mas completaa que topografia =D
0oe esta recontra entendible!!!!!!!!!!!!
Topografia .l.
Acaso no sabes leer? o simplemente eres imbécil?
El artículo está muy claro.
Saludos desde la Universidad de Chile.